
Background:
| 1. “Jesus’s Response to Dishonor“ 2. For Stephen King, August 11, 2009 3. Art and Man at Yale |

Background:
| 1. “Jesus’s Response to Dishonor“ 2. For Stephen King, August 11, 2009 3. Art and Man at Yale |
“When New Haven was founded, the city was laid out into a grid of nine squares surrounded by a great wilderness.
Last year [2000] History of Art Professor Emeritus Vincent Scully said the original town plan reflected a feeling that the new city should be sacred.
Scully said the colony’s founders thought of their new Puritan settlement as a ‘nine-square paradise on Earth, heaven on earth, New Haven, New Jerusalem.’”
– Yale Daily News, Jan. 11, 2001
“Real and unreal are two in one:
New Haven
Before and after one arrives….”
– Wallace Stevens,
“An Ordinary Evening
in New Haven,” XXVIII
See also Art and Man at Yale.
Sophists
From David Lavery’s weblog today–
Kierkegaard on Sophists:
“If the natural sciences had been developed in Socrates’ day as they are now, all the sophists would have been scientists. One would have hung a microscope outside his shop in order to attract customers, and then would have had a sign painted saying: Learn and see through a giant microscope how a man thinks (and on reading the advertisement Socrates would have said: that is how men who do not think behave).”– Søren Kierkegaard, Journals, edited and translated by Alexander Dru
To anyone familiar with Pirsig’s classic Zen and the Art of Motorcycle Maintenance, the above remarks of Kierkegaard ring false. Actually, the sophists as described by Pirsig are not at all like scientists, but rather like relativist purveyors of postmodern literary “theory.” According to Pirsig, the scientists are like Plato (and hence Socrates)– defenders of objective truth.
Pirsig on Sophists:
“The pre-Socratic philosophers mentioned so far all sought to establish a universal Immortal Principle in the external world they found around them. Their common effort united them into a group that may be called Cosmologists. They all agreed that such a principle existed but their disagreements as to what it was seemed irresolvable. The followers of Heraclitus insisted the Immortal Principle was change and motion. But Parmenides’ disciple, Zeno, proved through a series of paradoxes that any perception of motion and change is illusory. Reality had to be motionless.
The resolution of the arguments of the Cosmologists came from a new direction entirely, from a group Phædrus seemed to feel were early humanists. They were teachers, but what they sought to teach was not principles, but beliefs of men. Their object was not any single absolute truth, but the improvement of men. All principles, all truths, are relative, they said. ‘Man is the measure of all things.’ These were the famous teachers of ‘wisdom,’ the Sophists of ancient Greece.
To Phaedrus, this backlight from the conflict between the Sophists and the Cosmologists adds an entirely new dimension to the Dialogues of Plato. Socrates is not just expounding noble ideas in a vacuum. He is in the middle of a war between those who think truth is absolute and those who think truth is relative. He is fighting that war with everything he has. The Sophists are the enemy.
Now Plato’s hatred of the Sophists makes sense. He and Socrates are defending the Immortal Principle of the Cosmologists against what they consider to be the decadence of the Sophists. Truth. Knowledge. That which is independent of what anyone thinks about it. The ideal that Socrates died for. The ideal that Greece alone possesses for the first time in the history of the world. It is still a very fragile thing. It can disappear completely. Plato abhors and damns the Sophists without restraint, not because they are low and immoral people… there are obviously much lower and more immoral people in Greece he completely ignores. He damns them because they threaten mankind’s first beginning grasp of the idea of truth. That’s what it is all about.
The results of Socrates’ martyrdom and Plato’s unexcelled prose that followed are nothing less than the whole world of Western man as we know it. If the idea of truth had been allowed to perish unrediscovered by the Renaissance it’s unlikely that we would be much beyond the level of prehistoric man today. The ideas of science and technology and other systematically organized efforts of man are dead-centered on it. It is the nucleus of it all.
And yet, Phaedrus understands, what he is saying about Quality is somehow opposed to all this. It seems to agree much more closely with the Sophists.”
I agree with Plato’s (and Rebecca Goldstein’s) contempt for relativists. Yet Pirsig makes a very important point. It is not the scientists but rather the storytellers (not, mind you, the literary theorists) who sometimes seem to embody Quality.
As for hanging a sign outside the shop, I suggest (particularly to New Zealand’s Cullinane College) that either or both of the following pictures would be more suggestive of Quality than a microscope:

For the “primordial protomatter”
in the picture at left, see
The Diamond Archetype.
A note from 1985 leads,
via today’s earlier entry,
to an article from 1993:
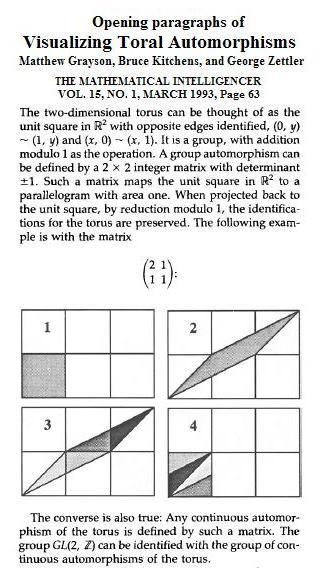
See also
Arnold’s Cat Map.
From a 1984 book review:
“After three decades of intensive research by hundreds of group theorists, the century old problem of the classification of the finite simple groups has been solved and the whole field has been drastically changed. A few years ago the one focus of attention was the program for the classification; now there are many active areas including the study of the connections between groups and geometries, sporadic groups and, especially, the representation theory. A spate of books on finite groups, of different breadths and on a variety of topics, has appeared, and it is a good time for this to happen. Moreover, the classification means that the view of the subject is quite different; even the most elementary treatment of groups should be modified, as we now know that all finite groups are made up of groups which, for the most part, are imitations of Lie groups using finite fields instead of the reals and complexes. The typical example of a finite group is
– Jonathan L. Alperin,
review of books on group theory,
Bulletin (New Series) of the American
Mathematical Society 10 (1984) 121, doi:
10.1090/S0273-0979-1984-15210-8

The same example
at Wolfram.com:
Citation data from Wolfram.com:
“GL(2,p) and GL(3,3) Acting on Points“
from The Wolfram Demonstrations Project,
http://demonstrations.wolfram.com/GL2PAndGL33ActingOnPoints/,
Contributed by: Ed Pegg Jr“
As well as displaying Cullinane’s 48 pictures of group actions from 1985, the Pegg program displays many, many more actions of small finite general linear groups over finite fields. It illustrates Cullinane’s 1985 statement:
“Actions of GL(2,p) on a p×p coordinate-array have the same sorts of symmetries, where p is any odd prime.”
Pegg’s program also illustrates actions on a cubical array– a 3×3×3 array acted on by GL(3,3). For some other actions on cubical arrays, see Cullinane’s Finite Geometry of the Square and Cube.
Prima Materia
(Background: Art Humor: Sein Feld (March 11, 2009) and Ides of March Sermon, 2009)
From Cardinal Manning’s review of Kirkman’s Philosophy Without Assumptions–
“And here I must confess… that between something and nothing I can find no intermediate except potentia, which does not mean force but possibility.”– Contemporary Review, Vol. 28 (June-November, 1876), page 1017
Furthermore….
Cardinal Manning, Contemporary Review, Vol. 28, pages 1026-1027:
The following will be, I believe, a correct statement of the Scholastic teaching:–1. By strict process of reason we demonstrate a First Existence, a First Cause, a First Mover; and that this Existence, Cause, and Mover is Intelligence and Power.
2. This Power is eternal, and from all eternity has been in its fullest amplitude; nothing in it is latent, dormant, or in germ: but its whole existence is in actu, that is, in actual perfection, and in complete expansion or actuality. In other words God is Actus Purus, in whose being nothing is potential, in potentia, but in Him all things potentially exist.
3. In the power of God, therefore, exists the original matter (prima materia) of all things; but that prima materia is pura potentia, a nihilo distincta, a mere potentiality or possibility; nevertheless, it is not a nothing, but a possible existence. When it is said that the prima materia of all things exists in the power of God, it does not mean that it is of the existence of God, which would involve Pantheism, but that its actual existence is possible.
4. Of things possible by the power of God, some come into actual existence, and their existence is determined by the impression of a form upon this materia prima. The form is the first act which determines the existence and the species of each, and this act is wrought by the will and power of God. By this union of form with the materia prima, the materia secunda or the materia signata is constituted.
5. This form is called forma substantialis because it determines the being of each existence, and is the root of all its properties and the cause of all its operations.
6. And yet the materia prima has no actual existence before the form is impressed. They come into existence simultaneously;
[p. 1027 begins]
as the voice and articulation, to use St. Augustine’s illustration, are simultaneous in speech.
7. In all existing things there are, therefore, two principles; the one active, which is the form– the other passive, which is the matter; but when united, they have a unity which determines the existence of the species. The form is that by which each is what it is.
8. It is the form that gives to each its unity of cohesion, its law, and its specific nature.*
When, therefore, we are asked whether matter exists or no, we answer, It is as certain that matter exists as that form exists; but all the phenomena which fall under sense prove the existence of the unity, cohesion, species, that is, of the form of each, and this is a proof that what was once in mere possibility is now in actual existence. It is, and that is both form and matter.
When we are further asked what is matter, we answer readily, It is not God, nor the substance of God; nor the presence of God arrayed in phenomena; nor the uncreated will of God veiled in a world of illusions, deluding us with shadows into the belief of substance: much less is it catter [pejorative term in the book under review], and still less is it nothing. It is a reality, the physical kind or nature of which is as unknown in its quiddity or quality as its existence is certainly known to the reason of man.
* “… its specific nature”
(Click to enlarge) –
For a more modern treatment of these topics, see Werner Heisenberg’s Physics and Philosophy. For instance:
“The probability wave of Bohr, Kramers, Slater, however, meant… a tendency for something. It was a quantitative version of the old concept of ‘potentia’ in Aristotelian philosophy. It introduced something standing in the middle between the idea of an event and the actual event, a strange kind of physical reality just in the middle between possibility and reality.”
Compare to Cardinal Manning’s statement above:
“… between something and nothing I can find no intermediate except potentia…”
To the mathematician, the cardinal’s statement suggests the set of real numbers between 1 and 0, inclusive, by which probabilities are measured. Mappings of purely physical events to this set of numbers are perhaps better described by applied mathematicians and physicists than by philosophers, theologians, or storytellers. (Cf. Voltaire’s mockery of possible-worlds philosophy and, more recently, The Onion‘s mockery of the fictional storyteller Fournier’s quantum flux. See also Mathematics and Narrative.)
Regarding events that are not purely physical– those that have meaning for mankind, and perhaps for God– events affecting conception, birth, life, and death– the remarks of applied mathematicians and physicists are often ignorant and obnoxious, and very often do more harm than good. For such meaningful events, the philosophers, theologians, and storytellers are better guides. See, for instance, the works of Jung and those of his school. Meaningful events sometimes (perhaps, to God, always) exhibit striking correspondences. For the study of such correspondences, the compact topological space [0, 1] discussed above is perhaps less helpful than the finite Galois field GF(64)– in its guise as the I Ching. Those who insist on dragging God into the picture may consult St. Augustine’s Day, 2006, and Hitler’s Still Point.
“… Kirkman has established an incontestable claim to be regarded as the founding father of the theory of designs.”
– “T.P. Kirkman, Mathematician,” by N.L. Biggs, Bulletin of the London Mathematical Society, Volume 13, Number 2 (March 1981), 97-120.
This paper is now available online for $12.
For more about this subject, see Design Theory, by Beth, Jungnickel, and Lenz, Cambridge U. Press, Volume I (2nd ed., 1999, 1120 pages) and Volume II (2nd ed., 2000, 513 pages).
For an apparently unrelated subject with the same name, see Graphic Design Theory: Readings from the Field, by Helen Armstrong (Princeton Architectural Press, 2009).
For what the two subjects have in common, see Block Designs in Art and Mathematics.
Recent Comments