May 23, 2007
-
Strong Emergence Illustrated:
The Beauty Test"There is no royal road
to geometry"
-- Attributed to EuclidThere are, however, various non-royal roads. One of these is indicated by yesterday's Pennsylvania lottery numbers:
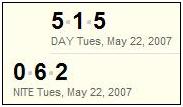 The mid-day number 515 may be taken as a reference to 5/15. (See the previous entry, "Angel in the Details," and 5/15.)The evening number 062, in the context of Monday's entry "No Royal Roads" and yesterday's "Jewel in the Crown,"
The mid-day number 515 may be taken as a reference to 5/15. (See the previous entry, "Angel in the Details," and 5/15.)The evening number 062, in the context of Monday's entry "No Royal Roads" and yesterday's "Jewel in the Crown,"
may be regarded as naming a non-royal road to geometry: either U. S. 62, a major route
from Mexico to Canada (home of the late geometer H.S.M. Coxeter), or a
road less traveled-- namely, page 62 in Coxeter's classic Introduction to Geometry (2nd ed.):
The illustration (and definition) is
of regular tessellations of the plane.This topic Coxeter offers as an
illustration of remarks by G. H. Hardy
that he quotes on the preceding page: One might argue that such beauty is strongly emergent
One might argue that such beauty is strongly emergent
because of the "harmonious way" the parts fit
together: the
regularity (or fitting together) of the whole is not reducible to the
regularity of the parts. (Regular triangles, squares, and
hexagons fit together, but regular pentagons do not.)The symmetries of these regular tessellations
of the
plane are less well suited as illustrations of emergence, since they
are tied rather closely to symmetries of the component parts.But the symmetries of regular tessellations of the sphere-- i.e., of the five Platonic solids-- do emerge strongly, being apparently independent of symmetries of the component parts.Another example of strong emergence: a group of 322,560 transformations acting naturally on the 4x4 square grid-- a much larger group than the group of 8 symmetries of each component (square) part.
The lottery numbers above also supply an example of strong emergence-- one that nicely illustrates how it can be, in the words of Mark Bedau, "uncomfortably like magic."
(Those more comfortable with magic may note the resemblance of the
central part of Coxeter's illustration to a magical counterpart-- the Ojo de Dios of Mexico's Sierra Madre.)
Recent Comments